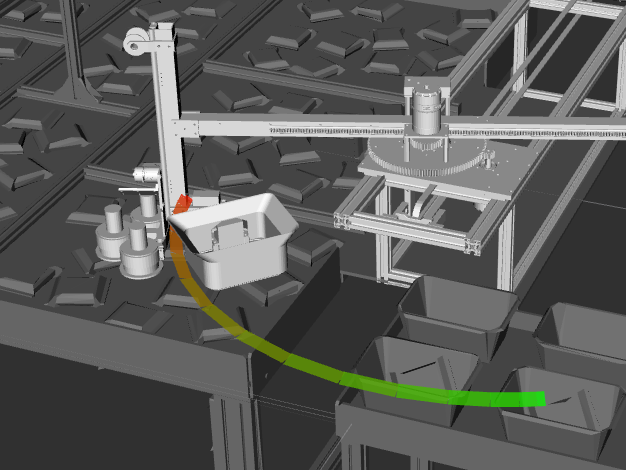
Pontryaginの最小原理を用いた軌道生成
Pontryaginの最小原理を用いて,2点境界値問題における評価関数を最小化する軌道を解析的に求めました。 障害物は考慮せず,計算コストを小さくする軌道生成を目的とします。

Pontryaginの最小原理を用いて,2点境界値問題における評価関数を最小化する軌道を解析的に求めました。 障害物は考慮せず,計算コストを小さくする軌道生成を目的とします。
9軸センサに拡張カルマンフィルタ(Extended Kalman Filter:EKF)を適用してクォータニオンを推定します。

プロペラを用いた倒立振子を製作しました。

PD制御を用いた3次元フライホイール倒立振子を製作しました。
Madgwickフィルタでクォータニオンを推定します。 加速度とジャイロを使ったMadgwickフィルタと,地磁気を考慮したMadgwickフィルタの2つを考えます。

状態空間表現を用いて,3次元フライホイール倒立振子を製作します。
6軸IMUと相補フィルタを用いてオイラー角を推定します。
相補フィルタはカルマンフィルタと同様の働きがあり,簡単で実用性が高いです。
状態空間表現を用いた,1次元フライホイール倒立振子の制御を説明します。
Kanayama Control Methodを用いてスラローム走行を設計します。
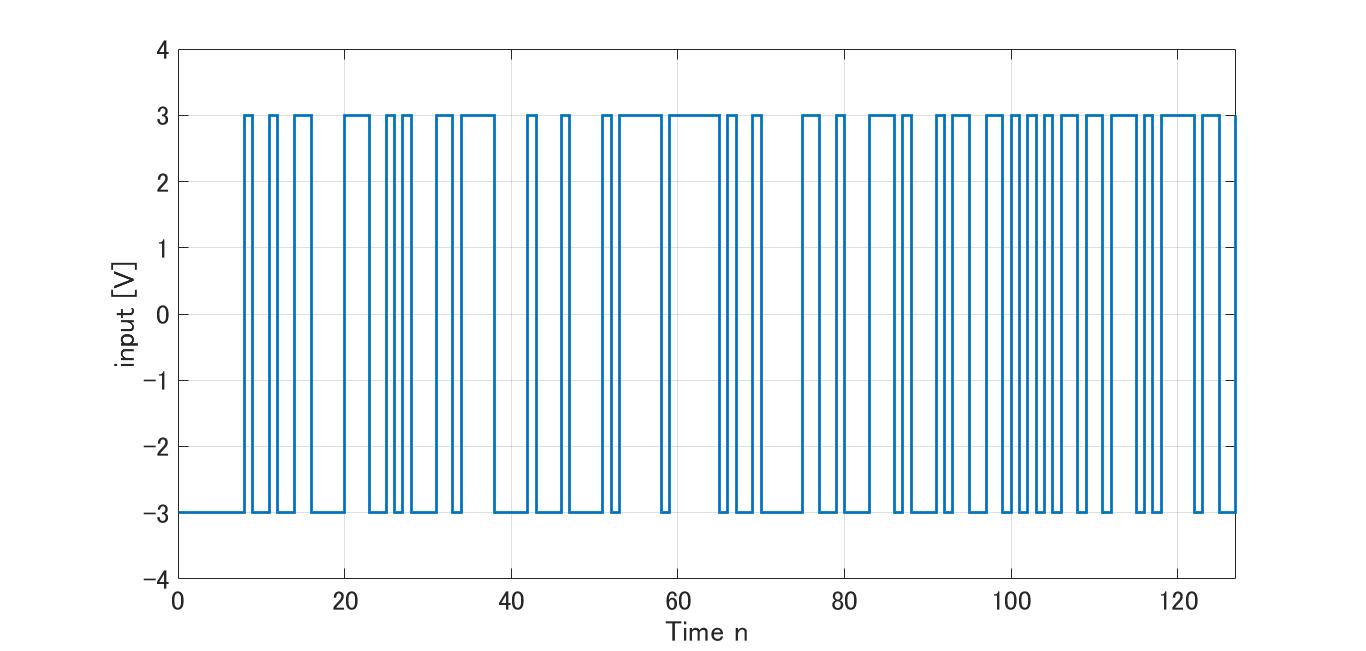
M系列信号を用いて回転方向のシステム同定をします。