Pontryaginの最小原理を用いた軌道生成
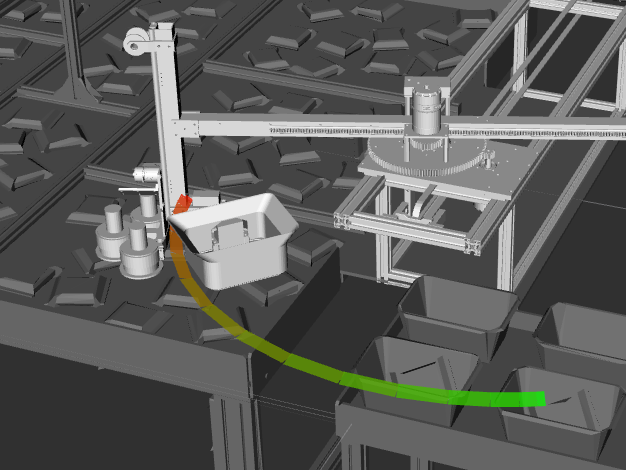
Pontryaginの最小原理を用いて,2点境界値問題における評価関数を最小化する軌道を解析的に求めました。 障害物は考慮せず,計算コストを小さくする軌道生成を目的とします。
1. 評価関数
評価関数は凸関数とします。 ここでは,評価関数をjerk(躍度)の2乗の時間平均
$$J=\dfrac{1}{T}\int_0^T\dddot{x}^2(t)dt$$
とします。 $T$は軌道の終端時刻であり,$0\leq t \leq T$です。 この評価関数$J$を最小化する軌道を,Pontryaginの最小原理を用いて求めます。
2. Hamiltonian
ここでは,$s=(s_1,s_2,s_3)=(x,\dot{x},\ddot{x})$,$u=\dddot{x}$とします。 簡単のために線形とし,対象のダイナミクスは考慮しません。
$$\dot{s}=(\dot{s}_1,\dot{s}_2,\dot{s}_3)=(s_2,s_3,u)$$
ステージコストと,随伴変数$\lambda=(\lambda_1,\lambda_2,\lambda_3)$を用いてHamiltonianを表現します。
$$H(s,u,\lambda)=\dfrac{1}{T}u^2+\lambda^T\dot{s}=\dfrac{1}{T}u^2+\lambda_1 s_2+\lambda_2 s_3+\lambda_3 u$$
3. Hamiltonianを最小化する$u$を求める
$$\nabla_uH(s,u,\lambda)=0$$
より,
$$\dfrac{2}{T}u+\lambda_3=0,\quad u=-\dfrac{T}{2}\lambda_3$$
となります。 随伴変数の$\lambda_3$が残っているので,随伴方程式を解いて求めていきます。
4. 随伴変数$\lambda$を求める
随伴方程式は,随伴変数の定義より $$\dot{\lambda}=-\nabla_sH(s,u,\lambda)$$ であり,これを解いて $$\dot{\lambda}=(0,-\lambda_1,-\lambda_2)$$
を満たすように$\lambda$を積分により求めると,
$$\lambda_1(t)=-\dfrac{2}{T}c_1$$
$$\lambda_2(t)=\dfrac{2}{T}(c_1t+c_2)$$
$$\lambda_3 = \dfrac{1}{T}(-c_1t^2-2c_2t-2c_3)$$
となります(積分定数は$u^*$を簡潔に書けるように選んでいます)。 この$\lambda_3$を3の$u$に代入すると,
$$u^*=\text{arg min }H(s,u,\lambda)=\dfrac{c_1}{2}t^2+c_2t+c_3$$
となり,この入力$u^*$は評価関数$J$を最小化する入力となります。
5. 目標軌道を求める
$u^*$を積分すれば$s_3(=\ddot{x})$,$s_3$を積分すれば$s_2(=\dot{x})$,$s_2$を積分すれば$s_1(=x)$となります。
$$s_1^*(t)=\dfrac{1}{120}c_1t^5+\dfrac{1}{24}c_2t^4+\dfrac{1}{6}c_3t^3+\dfrac{1}{2}c_4t^2+c_5t+c_6$$
$$s_2^*(t)=\dfrac{1}{24}c_1t^4+\dfrac{1}{6}c_2t^3+\dfrac{1}{2}c_3t^2+c_4t+c_5$$
$$s_3^*(t)=\dfrac{1}{6}c_1t^3+\dfrac{1}{2}c_2t^2+c_3t+c_4$$
6. 目標軌道の係数を求める
初期と終端の条件,軌道時間を与えてあげると,連立方程式を解くだけでパラメータ$c_1\sim c_6$が求まります。 ここでは例として,ある位置$x_0$での静止状態から,$x_T$への静止状態に遷移することを考えます。 $$s_1(0)=x_0,\quad s_2(0)=0,\quad s_3(0)=0$$
$$s_1(T)=x_T,\quad s_2(T)=0,\quad s_3(T)=0$$
として1.5の方程式を解くと,
$$ \begin{bmatrix} c_4\\ c_5\\ c_6 \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ x_0 \end{bmatrix} $$ $$ \begin{bmatrix} c_1\\ c_2\\ c_3 \end{bmatrix} =\dfrac{1}{T^5} \begin{bmatrix} 720\\ -360T\\ 60T^2 \end{bmatrix} (x_T-x_0) $$となりました。 軌道生成時には,まず条件を渡して$c_1\sim c_6$のパラメータを決定し,次に$s_1,s_2,s_3$の時間軌道を一意に求めるということになります。
7. 実践
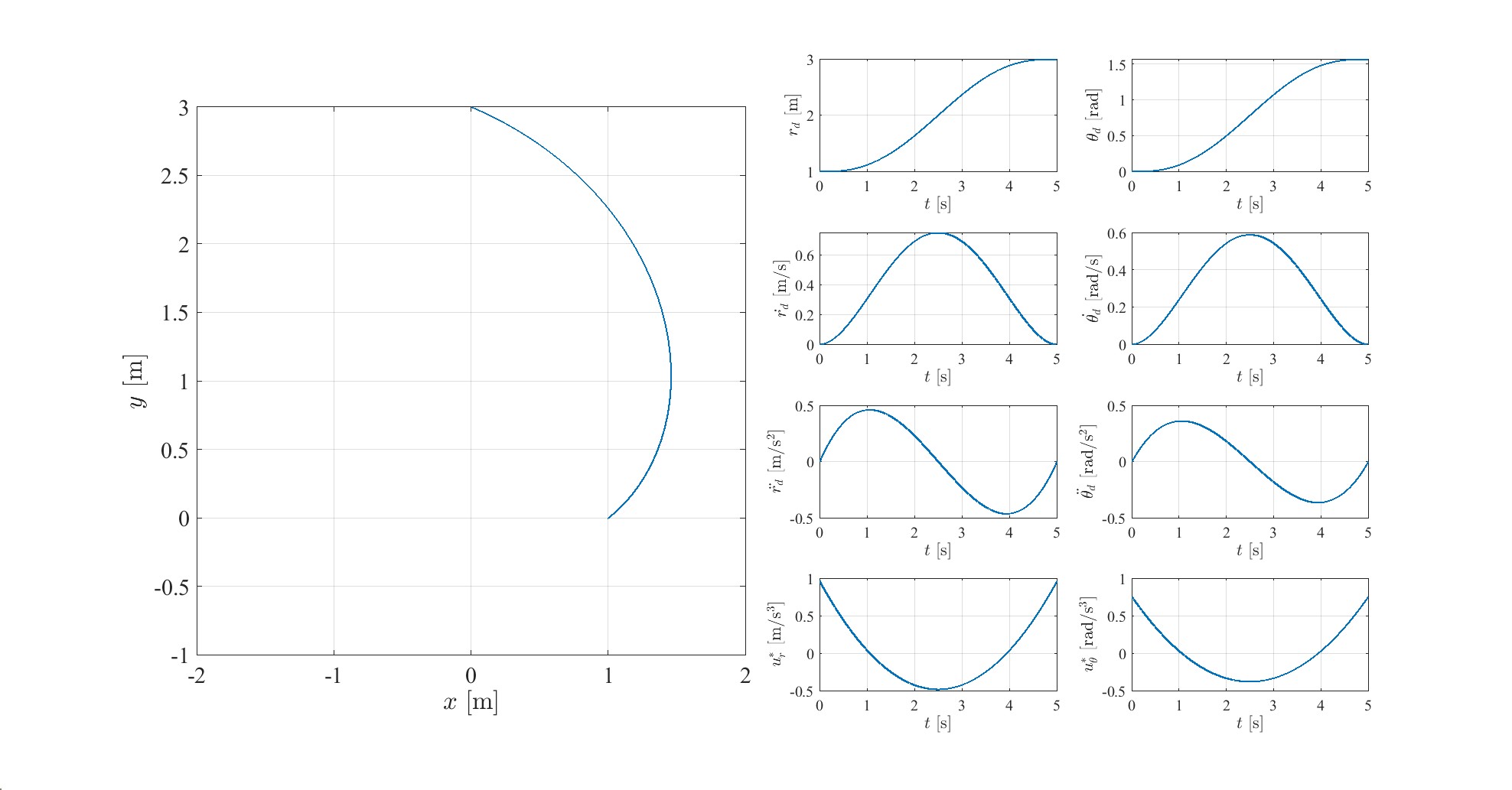
$r$と$\theta$が制御できる極座標系のロボットを対象とします。 $xy$座標上の経路は考慮せず,$r$と$\theta$それぞれにおいて独立して軌道を考えます。
- MATLABでのシミュレーション
- ROS2での実装とRvizでの可視化($r$と$\theta$に加えて$x$のアクチュエータを追加)
- 実機実験と一部ログ
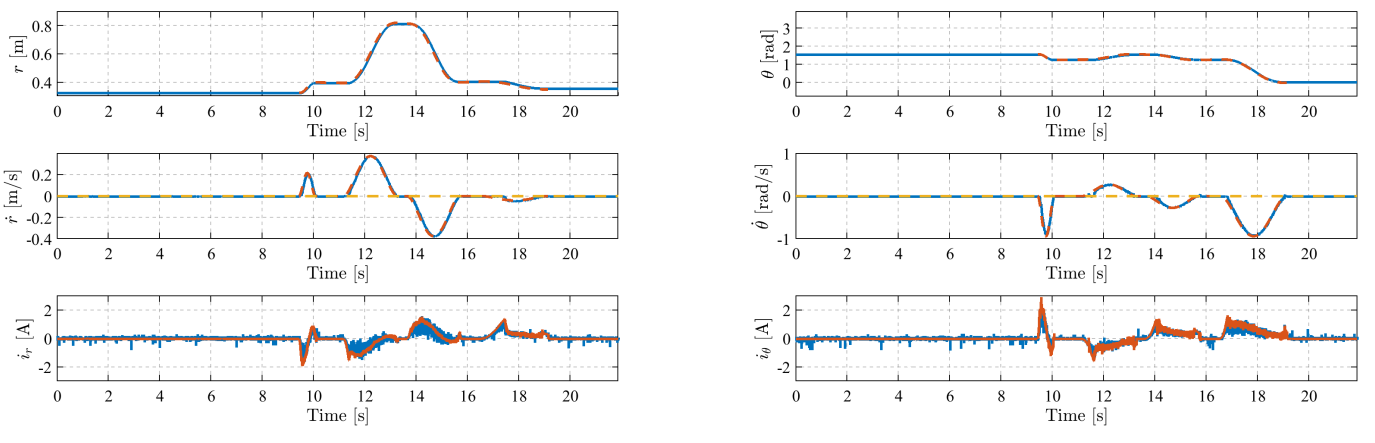
生成した位置と速度軌道はフィードバックに,加速度の軌道はフィードフォワードに利用し,電流入力で制御しています。 青が測定値,赤が目標値で,綺麗に軌道追従させることができました。
