Z変換を用いた正弦波の生成

October 18, 2023

今ではマイコンで$\sin(),\ \cos()$関数が簡単に実装でき，DSPでも高速処理できます。一方ではz変換を用いて処理を高速化する手法もあります。

ここでは勉強のため，z変換を用いて正弦波を生成します。

正弦波を$h(t)=a\sin(\omega t)$とし，サンプリング間隔$T$で離散化した$h(nT)=a\sin(n\omega T)$を$z$変換します。

$$ \begin{align*} H(z)=\sum_{n=0}^{\infty}h(nT)z^{-n}=\dfrac{a\sin(\omega T)z^{-1}}{1-2\cos(\omega T)z^{-1}+z^{-2}} \end{align*} $$

$z$変換して得た伝達関数$H(z)$を用いて，インパルス応答を求めます。このインパルス応答が正弦波となります。

$$ \begin{align*} Y(z) = H(z)X(z)=\dfrac{a\sin(\omega T)z^{-1}}{1-2\cos(\omega T)z^{-1}+z^{-2}}X(z) \end{align*} $$

$$ Y(z)=2\cos(\omega T)Y(z)z^{-1}-Y(z)z^{-2}+a\sin(\omega T)X(z)z^{-1} $$

$$ y(nT)=2\cos(\omega T)y((n-1)T)-y((n-2)T)+a\sin(\omega T)x((n-1)T) $$

ただし，$x(nT)$はインパルス入力であり，ここでは

$$ \begin{equation*} \left\{ \, \begin{aligned} & x(b)=1 \\ & x(nT)=0\quad (n\neq b) \end{aligned} \right. \end{equation*} $$

とします。

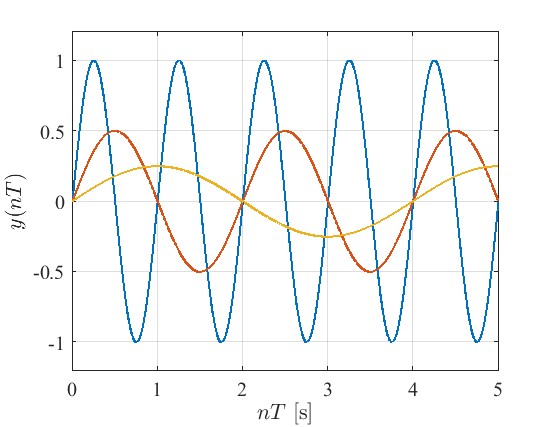
$a,b,\omega,T,y(0)$を変えてMATLABで正弦波を生成しました。

振幅と周波数を変えたもので，綺麗に正弦波が生成されています。

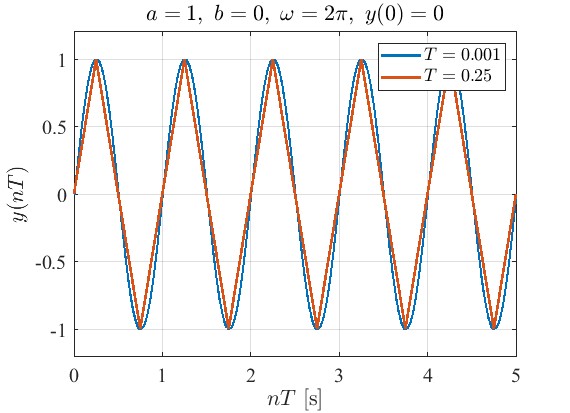
サンプリング周期$T$を変更しました。$T=0.25$の場合は目的の$1$[Hz]の周波数に対して，サンプリングが$4$[Hz]なので三角波になります。$T$を荒くしすぎると正弦波から離れていくことが分かります。

インパルス入力の遅れ$b$を変更しました。入力遅れを入れれば位相差が生じます。

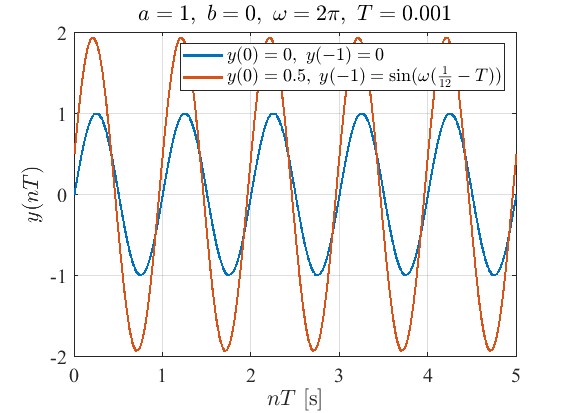
初期値$y(0)$を変更し，それに合わせて$y(-1)$も変更しました。当然ですが，初期値が$y(0)=0,\ y(-1)=0$ではない状態でインパルス入力を加えると，振幅がずれます。

また，初期値を変更した上でインパルス入力を加えなければ，位相差のみがある正弦波が生じます。

z変換を用いて正弦波を生成し，パラメータを変えた際の出力結果を確認しました。マイコンで実装されていて簡単に使える三角関数が，いかに便利であるか分かります。