プロペラを用いた倒立振子の製作

プロペラを用いた倒立振子を製作しました。
Design, Modeling and Control of an Omni-Directional Aerial Vehicle を参考にしています。
以下は以前に作成した説明スライドです。開発していく上で変更した点はありますが,説明していきます。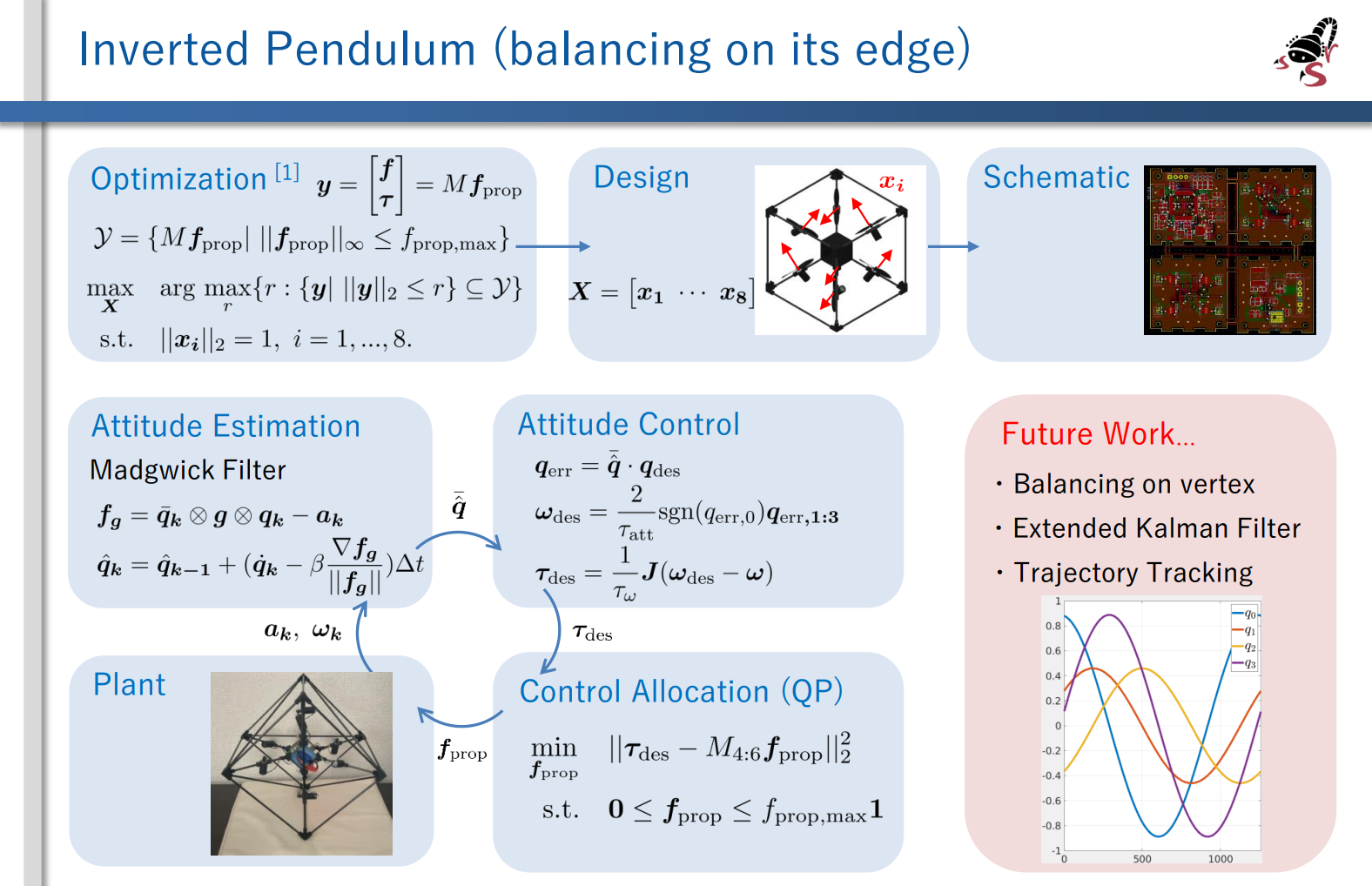
1. プロペラの方向最適化
最初に記述した参考文献ではプロペラの方向が最適化されています。
$$ y=\begin{bmatrix} f \\ \tau \end{bmatrix}=Mf_{\text{prop}}, \quad f=\begin{bmatrix} f_x\\ f_y\\ f_z \end{bmatrix},\quad \tau=\begin{bmatrix} \tau_x\\ \tau_y\\ \tau_z \end{bmatrix},\quad f_{\text{prop}}=\begin{bmatrix} f_{\text{prop},1}\\ f_{\text{prop},2}\\ \vdots\\ f_{\text{prop},8}\\ \end{bmatrix} $$ $$ \mathcal{Y}=\{Mf_{\text{prop}}|\ ||f_{\text{prop}}||_\infty\leq f_{\text{prop,max}}\} $$ \begin{align*} \underset{X}{\text{max}} & \quad \text{arg}\ \underset{r}{\text{max}}\{r:\{y|\ ||y||_2\leq r\}\subseteq\mathcal{Y}\} \\ \mathrm{s.t.} & \quad ||x_i||_2=1,\ i=1,...,8. \end{align*}$x_i$は各プロペラの方向,$X$は$x_i$をならべた行列,$M$はプロペラの位置と方向によって決まる行列です。 $\mathcal{Y}$は機体が出力できる力とトルクの集合で,プロペラの位置を固定した上で力とトルクのL2ノルムが最大になるようにプロペラ方向を最適化しています。
今回は倒立振子を考えるので,回転中心は重心ではなく立方体の頂点です。 また,目的は倒立なので頂点にかかる力は考える必要がありません。 そのため,この方向最適化は倒立には不適切ですが,倒立に要するトルクは十分足りているとしています。
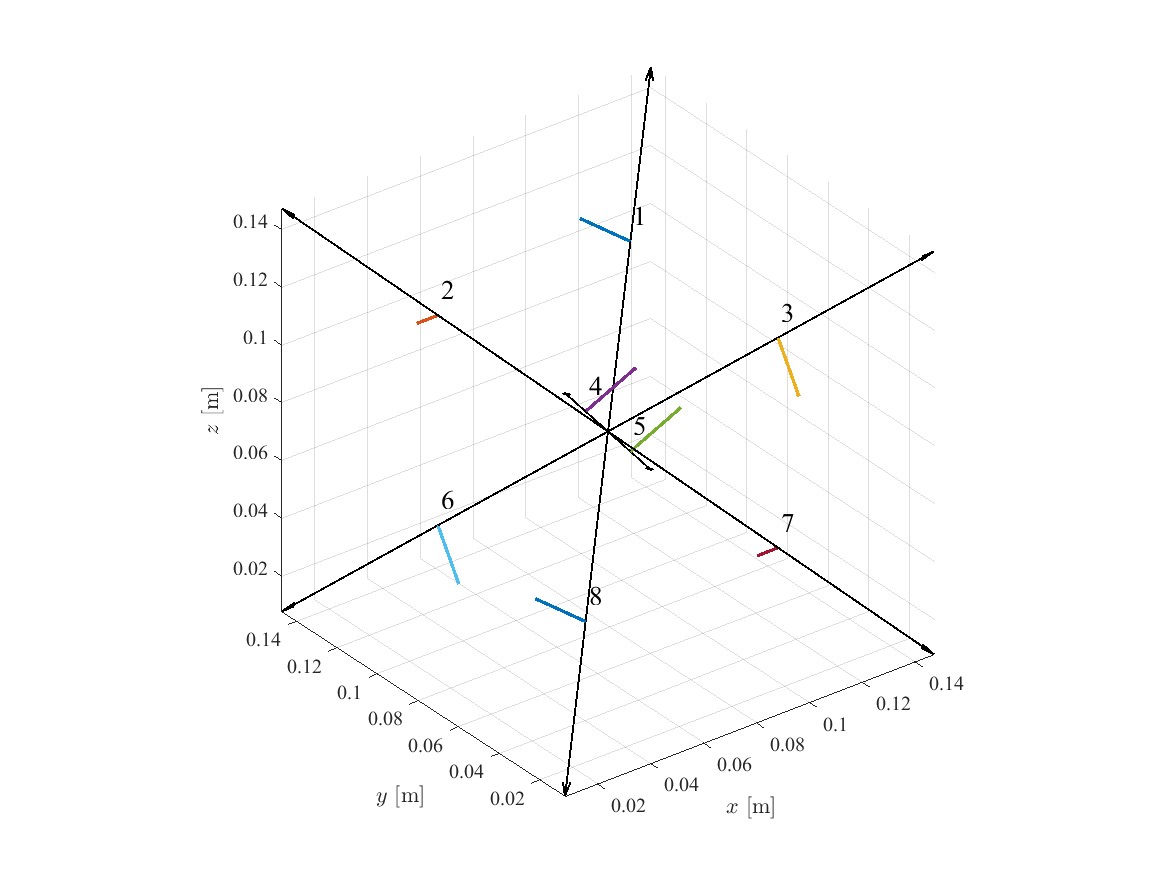
Propeller Direction

Torque Set
2. 機体作成

| マイコン | STM32F446RE |
| IMU | MPU-9250 |
| モータ | 小型ドローン用DCモータ × 8 |
| 電源 | Lipo 2S 240mAh |
カーボンロッドを繋いで立方体としています。 回路基板は4枚で,組み合わせて小さな立方体になるようにしました。
3. 姿勢推定
以下の2つを実装して,どちらかを使うようにしています。
- Madgwick Filter
- Extended Kalman Filter (EKF)
Madgwickフィルタでクォータニオンを推定する・ EKFでクォータニオンを推定する に記述しています。
4. 姿勢制御
- Nonlinear Attitude Control
参考文献に載っていたもので,クォータニオンを用いた制御です。
$$ q_{\text{err}}=\bar{q}\cdot q_{\text{des}} $$
$$ \omega_{\text{des}}=\dfrac{2}{\tau_{\text{att}}}\text{sgn}(q_{\text{err},0})q_{\text{err},1:3} $$
$$ \tau_{\text{des}}=\dfrac{1}{\tau_\omega}J(\omega_{\text{des}}-\omega) $$
$\tau_{\text{att}},\tau_\omega$は時定数,$J$は回転軸周りの慣性モーメントです。 角速度$\omega_{\text{des}}$の求め方ですが,Lyapnov安定となるように制御設計されています。
- Linear Quadratic Regulator (LQR)
状態方程式を求め,線形化してLQRを用いる制御です。 辺倒立では,状態をピッチ角$\theta$とその速度$\dot\theta$として状態方程式を立て,倒立点近傍で線形化しました。この場合,実質PD制御となります。
- PD制御
辺倒立では実際にはピッチ角$\theta$のPD制御を用いています。
$$ \tau_{\text{des},y} = k_p(\theta_{\text{des}}-\theta)+k_d(0-\omega_y) $$
モデル誤差の影響によりLQRでは不安定な場合が多かったため,PD制御でゲインを調整して倒立させました。
5. 推力配分
姿勢制御で求めたトルク入力$\tau_{\text{des}}$を満たすように,8つのプロペラ推力に配分します。
倒立点を原点とした,各プロペラの位置ベクトル$p_i$をならべた行列を$P$とすると, トルクとプロペラの推力の関係式を
$$ \tau= (P\times X) f_\text{prop}=M_\tau f_\text{prop} $$とします。プロペラの推力$f_\text{prop}$を $$ \tau_{\text{des}}=M_\tau f_\text{prop} $$ となるように求めたいのですが,推力には上限があるので$f_{\text{prop},i}<f_{\text{prop},\text{max}}$ となる必要があります。
そこで,制約付き2次計画問題を解くことにしました。
\begin{align*} \underset{f_{\text{prop}}}{\text{min}} & \quad (\tau_{\text{des}}-M_\tau f_\text{prop})^TQ(\tau_{\text{des}}-M_\tau f_\text{prop}) \\ \mathrm{s.t.} &\quad 0\leq f_{\text{prop},i}\leq f_{\text{prop},\text{max}},\quad i = 1,2,\cdots,8 \end{align*}ここで,
$$ Q=\begin{bmatrix} Q_{11} & 0 & 0\\ 0 & Q_{22} & 0\\ 0 & 0 & Q_{33} \end{bmatrix}>0 $$であり,辺倒立の場合は$x,z$軸周りのトルクは無視して$Q_{11}=Q_{33} = 0$としています。
実装では,CVXGENを用いて2次計画問題を解いています。
