地磁気センサのキャリブレーションをする
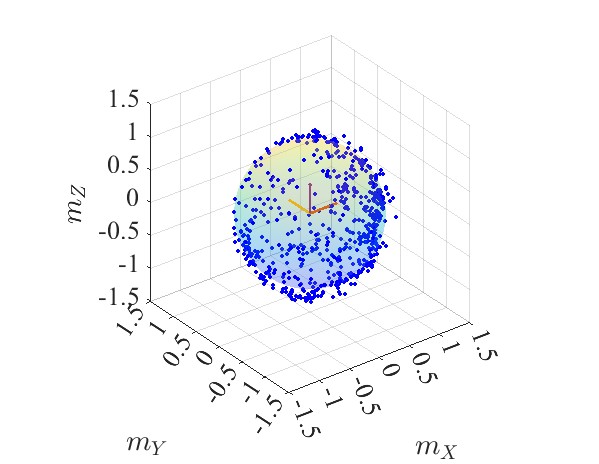
センサから取得する地磁気のキャリブレーションをしました。
今回,センサにはMPU9250を用いました。
地磁気センサ校正のための楕円体のパラメータ推定における最小二乗法
を参考にしています。
1. 最小二乗法を用いてデータを楕円体に近似する
楕円体の方程式は $$ a_{11}x^2+a_{22}y^2+a_{33}z^2+2a_{12}xy+2a_{23}yz+2a_{13}zx+b_1x+b_2y+b_3z+1=0 $$ であり,実際に得られるデータを元に最小二乗法を用いて$a_{ij},b_i$を求めます。
$x,y,z$軸において各$n(\geq9)$個のデータを得るとして,次の方程式を考えます。
$$ \left[ \begin{matrix} x(1)^2 & y(1)^2 & z(1)^2 & 2x(1)y(1) & 2y(1)z(1) & 2z(1)x(1) & x(1) & y(1) & z(1)\\ x(2)^2 & y(2)^2 & z(2)^2 & 2x(2)y(2) & 2y(2)z(2) & 2z(2)x(2) & x(2) & y(2) & z(2)\\ & & & &\vdots & & & &\\ x(n)^2 & y(n)^2 & z(n)^2 & 2x(n)y(n) & 2y(n)z(n) & 2z(n)x(n) & x(n) & y(n) & z(n)\\ \end{matrix} \right] \left[ \begin{matrix} a_{11} \\ a_{22} \\ a_{33} \\ a_{12} \\ a_{23} \\ a_{13} \\ b_1\\ b_2\\ b_3 \end{matrix} \right]= \left[ \begin{matrix} -1\\ -1\\ \vdots\\ -1\\ \end{matrix} \right] $$上式を$Mw=I$とおき,最小二乗法を用いて $$ w = M^\dagger I=(M^\text{T}M)^{-1}M^\text{T}I $$ とすることで楕円体を近似することができます。

2. 回転・移動・伸縮によって単位球とする
参考にした記事の通りに,回転・移動・伸縮をします。
$$ X = S\bigg(P^\text{T}x+\dfrac{1}{2}\Lambda^{-1}(BP)^\text{T}\bigg) $$
センサで取得した地磁気$x=(m_x, m_y,m_z)$に対して,回転$P^\text{T}$,移動$\dfrac{1}{2}\Lambda^{-1}(BP)^\text{T}$,伸縮$S$を施します。

地磁気センサのキャリブレーションができました。 地磁気を用いたMadgwick Filter,EKFといった姿勢推定をする際に活用します。
