曲線加速を用いた超信地旋回

March 22, 2022

曲線加速を用いて超信地旋回の設計をしました。

$\dfrac{\pi}{2}$だけ超信地旋回する際の曲線加速の設計に適用します。

1. 目標値の関数を求める

角躍度, 角加速度, 角速度, 角度の目標値をそれぞれ$j_{ref}(t), a_{ref}(t), \omega_{ref}(t), \theta_{ref}(t)$ とします。

$$ \begin{align} j_{ref}(t) & := \left\{ \begin{array}{ll} j_m & (0 < t \le t_1) \\ 0 & (t_1 < t \le t_2) \\ -j_m & (t_2 < t \le t_3) \\ \end{array} \right. \\ a_{ref}(t) & := \left\{ \begin{array}{ll} j_mt & (0 < t \le t_1) \\ a_m & (t_1 < t \le t_2) \\ -j_m(t-t_2) & (t_2 < t \le t_3) \\ \end{array} \right. \\ \omega_{ref}(t) & := \left\{ \begin{array}{ll} \frac{1}{2}j_mt^2 & (0 < t \le t_1) \\ \omega_1 + a_m(t-t_1) & (t_1 < t \le t_2) \\ \omega_3 - \frac{1}{2}j_m(t-t_3)^2 & (t_2 < t \le t_3) \end{array} \right. \\ \theta_{ref}(t) & := \left\{ \begin{array}{ll} \frac{1}{6}j_mt^3 & (0 < t \le t_1) \\ \theta_1 + \omega_1(t-t_1) + \frac{1}{2}a_m(t-t_1)^2 & (t_1 < t \le t_2) \\ \theta_2 + \omega_3(t-t_2) - \frac{1}{6}j_m(t-t_2)^3 & (t_2 < t \le t_3) \\ \end{array} \right. \end{align} $$

2. パラメータを決定する

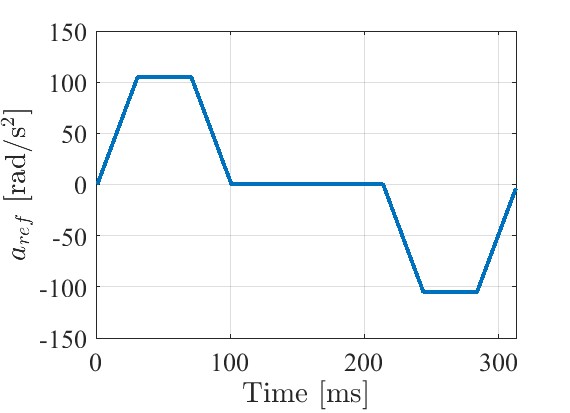
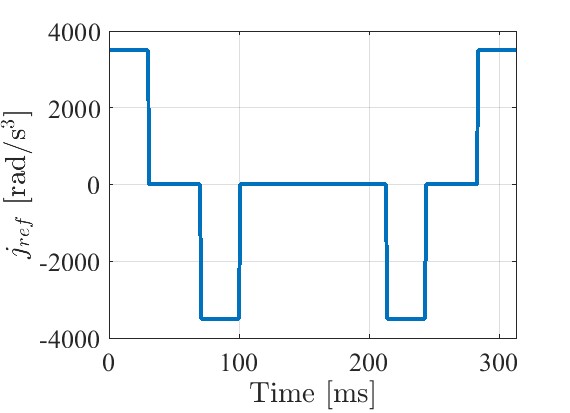
$t_1,t_2,t_3,j_m,a_m$を決定します。(ただし, $t_1=t_3-t_2=\dfrac{a_m}{j_m}$)

とりあえずMATLABで描画しながら次のようにパラメータを決定しました。

$$t_1=0.03[s]$$

$$t_2=0.07[s]$$

$$t_3=0.1[s]$$

$$j_m=3500[rad/s^3]$$

$$a_m=105[rad/s^2]$$

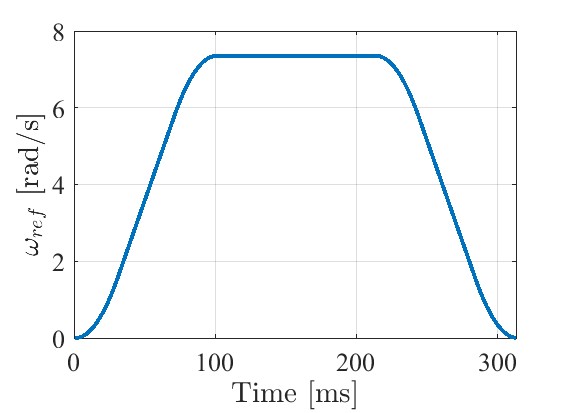
これらを決定したとき$\omega_3=7.35[rad/s]$となりました。

3. 角速度の積分値が$\dfrac{\pi}{2}$となるように設計する

最大（一定）角速度$\omega_3$である時間で回転角を調整します。時刻$t_4$まで$\omega_3$であるとすると, 角速度の積分値となる面積$S$は次式で表されます。

$$S=2\left\{\omega_1(t_2-t_1)+\dfrac{1}{2}a_m(t_2-t_1)^2+\omega_3(t_3-t_2)\right\}+\omega_3(t_4-t_3)$$

$S=\dfrac{\pi}{2}$となるように$t_4=213[ms]$と求めました。 $t_4は$整数で求まらなかったので四捨五入しました。

$\pi$回転する超信地旋回では$S=\pi$として$t_4$を求めます。

4. マイコンで目標値を生成する

マイコンで生成した目標値をMATLABでplotしました。

角速度

角加速度

角躍度

5. 2自由度制御を設計する

まず, 回転方向のシステム同定をします。同定については以下の記事を参考にさせていただきました。

マイクロマウスの機体を同定する

MATLABでマイクロマウスの機体をシステム同定してPIDチューニングする

1次の極をもつとして同定しました。 $$P_M(s)=\dfrac{K}{bs+1}$$ 2自由度制御によって目標値に追従させることにします。 $P_M^{-1}(s)$は非プロパーなので, 理論上では1次のフィルタを入れるなどしてフィードフォワードコントローラをプロパーにする必要がありますが, とりあえずフィルタを入れずに$F(s)=1$として考えます。

フィードバック

角速度の誤差にPID制御をかけます。 $$e_{\omega}=\omega_{ref}-\omega$$

$$u_{fb}=C(s)e_\omega=(k_{p_\omega}+k_{i_\omega}\dfrac{1}{s}+k_{d_\omega}\dfrac{s}{\tau s+1})e_{\omega}$$

フィードフォワード

フィードバックのみでは遅れがあるので, フィードフォワードを加えます。 $$u_{ff}=\omega_{ref}P_M^{-1}(s)=\omega_{ref}\dfrac{bs+1}{K}=\dfrac{ba_{ref}+\omega_{ref}}{K}$$

2自由度制御

$$u_{\omega}=u_{ff}+u_{fb}$$ 実際にはシステムを後退差分 $z=\dfrac{1}{1-Ts}$ で離散化しました。