IIRフィルタの設計

低域のIIRフィルタを設計し、ジャイロセンサに適用します。ここではまずプロトタイプフィルタを考え、双1次z変換によって目的のディジタルフィルタを求める手法を用います。

1. 設計仕様を与える

カットオフ周波数 $f_c=100\ [\text{Hz}]$、阻止域端周波数 $f_s=300\ [\text{Hz}]$、阻止域減衰量 $A_s=30\ [\text{dB}]$とします。

2. 正規化角周波数を求める

$f_c, f_s$は非正規化周波数であり, サンプリング周波数$F_s$を$1$とするように正規化して扱う必要があります.

ここでは, サンプリング周波数$F_s=1\ [\text{kHz}]$として正規化します。$f_c, f_s$に対応する正規化角周波数$\omega_c, \omega_s$は次のようになります。

$$\omega_c=2\pi \dfrac{f_c}{F_s}=0.2\pi\ [\text{rad}]$$

$$\omega_s=2\pi \dfrac{f_s}{F_s}=0.6\pi\ [\text{rad}]$$

3. プリワーピングをする

双1次z変換ではアナログフィルタの周波数 $\Omega=-\infty〜\infty$の範囲をディジタルフィルタの周波数 $\omega=-\pi〜\pi$の範囲に対応させるため, 周波数のひずみ（ワーピング）が生じます。そのため, ディジタルフィルタでの設計仕様 $\omega_c, \omega_s$を, アナログフィルタでの設計仕様となるように対応させる必要があります。これをプリワーピングといいます。ひずみが生じても設計仕様を満たすように前もってひずみをもたせておく, ということです。

周波数のひずみについて考えます。双1次z変換は次式で表されます.

$$s=2\dfrac{1-z^{-1}}{1+z^{-1}}$$

$s=j\Omega,\ z=e^{j\omega}$として周波数軸で考えると

$$j\Omega=2\dfrac{1-e^{-j\omega}}{1+e^{-j\omega}}$$

となり, 周波数のひずみは

$$\Omega=2\text{tan}\dfrac{\omega}{2}$$

となります。$\omega_c, \omega_s$をプリワーピングしてアナログフィルタでの設計仕様$\Omega_c, \Omega_s$とします。

$$\Omega_c=2\text{tan}\dfrac{\omega_c}{2},\ \Omega_s=2\text{tan}\dfrac{\omega_s}{2}$$

4. プロトタイプフィルタを求める

まず, ディジタルフィルタの設計の基礎となるアナログフィルタであるプロトタイプフィルタを考えます。 ここでは, バタワース低域フィルタを用いることにします。プロトタイプフィルタを1回求めておけば, 周波数変換によって所望のカットオフ周波数のディジタルフィルタに変更することもできます。

バタワース低域フィルタの設計では, 理想低域フィルタの特性に近似するために次の振幅特性が用いられます。 $N$はフィルタの次数です。

$$|H_a(j\Omega)|=\frac{1}{\sqrt{1+\bigg(\dfrac{\Omega}{\Omega_c}\bigg)^{2N}}}$$

設計仕様を満たすことができる次数$N$を求めます。$\Omega_s$における振幅が$A_s$より減衰していればよいので,

$$|H_a(j\Omega_s)|=\frac{1}{\sqrt{1+\bigg(\dfrac{\Omega_s}{\Omega_c}\bigg)^{2N}}}$$ $$A_s=-20\ \text{log}_{10}|H_a(j\Omega_s)|=10\ \text{log}_{10}\left\{1+\bigg(\dfrac{\Omega_s}{\Omega_c}\bigg)^{2N}\right\}$$ $$N=\dfrac{1}{2}\dfrac{\text{log}_{10}(10^{\frac{A_s}{10}}-1)}{\text{log}_{10}\bigg(\dfrac{\Omega_s}{\Omega_c}\bigg)}$$

このようにしてプロトタイプフィルタの次数$N$が求まります。$N$は切り上げて整数とします。

$N=3$と求まり, プロトタイプフィルタは次のようになりました。

$$H_a(s)=\dfrac{0.2744}{s^3+1.2997s^2+0.8446s+0.2744}$$

振幅特性は下図の通りです。

5. 双1次z変換で目的のディジタルフィルタを求める

求めたプロトタイプフィルタに双1次z変換を適用します。

$$H(z)=H_a(s)|_{s=2\frac{1-z^{-1}}{1+z^{-1}}}=\dfrac{0.0181+0.0543z^{-1}+0.0543z^{-2}+0.0181z^{-3}}{1-1.76z^{-1}+1.1829z^{-2}-0.2781z^{-3}}$$

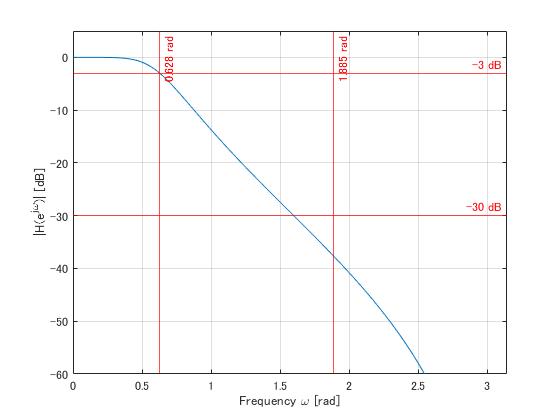
振幅特性は下図の通りです。

カットオフ周波数に対応する$\omega_c=0.2\pi\approx0.628\ [\text{rad}]$における減衰は$3\ [\text{dB}]$となっています。

阻止域端周波数に対応する$\omega_s=0.6\pi\approx1.885\ [\text{rad}]$における減衰量は$A_s=30\ [\text{dB}]$よりも大きいので問題ないです。一致しないのはフィルタ次数$N$を切り上げたためだと考えられます。

6. 実際にフィルタリングする

$x(n),\ y(n)$をそれぞれ時刻$n$での測定値, フィルタをかけた値とします。時刻$n$でのフィルタをかけた値は次式から求まります。

$$y(n)=0.0181x(n)+0.0543x(n-1)+0.0543x(n-2)+0.0181x(n-3) \\ +1.76y(n-1)-1.1829y(n-2)+0.2781y(n-3)$$